题目

Description

Bean-eating is an interesting game, everyone owns an M*N matrix, which is filled with different qualities beans. Meantime, there is only one bean in any 1*1 grid. Now you want to eat the beans and collect the qualities, but everyone must obey by the following rules: if you eat the bean at the coordinate(x, y), you can’t eat the beans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), and the both rows whose abscissas are x-1 and x+1.

Now, how much qualities can you eat and then get

Input

There are a few cases. In each case, there are two integer M (row number) and N (column number). The next M lines each contain N integers, representing the qualities of the beans. We can make sure that the quality of bean isn't beyond 1000, and 1<=M*N<=200000.

Output

For each case, you just output the MAX qualities you can eat and then get.

Sample Input

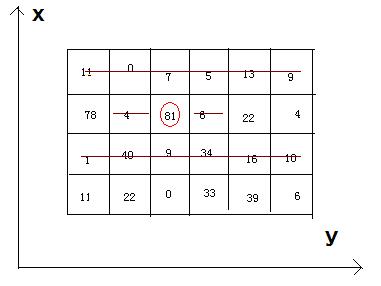
4 6
11 0 7 5 13 9
78 4 81 6 22 4
1 40 9 34 16 10
11 22 0 33 39 6

Sample Output

242

翻译

背景

吃豆子是一个有趣的游戏,每个人都拥有一个 M * N 矩阵,这里充满了不同质量豆子
每个网格中只有一个豆子
任务是收集最多的豆子
但必须遵守以下规则:
如果吃了坐标是 (x,y) 的豆子,则不能吃以下坐标的豆子(如果存在):
(x,y-1) , (x,y + 1) ,横坐标为 x - 1 , x + 1 的两行

输入

多组数据输入
每组数据先输入格数 M 、 N 分别代表 M 行 N 列
接下来 M 行每行有 N 个数,代表这个格子豆子的质量
豆子的质量小于 1000
1<=N*M<=200000

题解

>最大不连续子序列<

对于每一行,需要找出该行的最大不连续子序列
记录下每行这个最大的值

再对于整个图,在每行的最大值中,找出最大不连续子序列
此时求得的数,就是我们需要的答案

代码

/*
By:OhYee
Github:OhYee
HomePage:http://www.oyohyee.com
Email:oyohyee@oyohyee.com

かしこいかわいい？
エリーチカ！
要写出来Хорошо的代码哦~
*/

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <string>
#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
using namespace std;

const int maxn = 200005;
int numt[maxn];
int num[maxn];
int dp[maxn];
int N,M;

bool Do() {
    if(scanf("%d%d",&N,&M) == EOF)
        return false;

    memset(dp,0,sizeof(dp));

    for(int i = 1;i <= N;i++) {
        for(int j = 1;j <= M;j++) {
            int temp;
            scanf("%d",&temp);
            if(j <= 2) {
                if(j == 1)
                    numt[j] = temp;
                else
                    numt[j] = max(numt[1],temp);
            } else {
                numt[j] = max(numt[j - 1],numt[j - 2] + temp);
            }
        }
        num[i] = numt[M];
    }

    dp[1] = num[1];
    dp[2] = max(num[1],num[2]);
    for(int i = 3;i <= N;i++) {
        dp[i] = max(dp[i - 1],dp[i - 2] + num[i]);
    }

    printf("%d\n",dp[N]);
    return true;
}

int main() {
    while(Do());
    return 0;
}