题目

Description

Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.

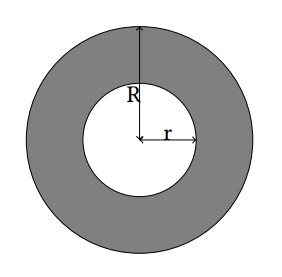
A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.

Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.

Input

The first line contains only one integer T (T ≤ 10 5), which indicates the number of test cases. For each test case, the first line contains two integers r, R (0 ≤ r < R ≤ 10).

Each of the following two lines contains two integers x i, y i (0 ≤ x i, y i ≤ 20) indicating the coordinates of the center of each ring.

Output

For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.

Sample Input

2
2 3
0 0
0 0
2 3
0 0
5 0

Sample Output

Case #1: 15.707963
Case #2: 2.250778

题解

纯数学公式推导题
由于牵扯的小数,需要使用 double 进行运算
由于会涉及浮点误差
因此在比较大小的时候需要注意把较大数加上一个偏移量

貌似用海伦公式会出现问题,最好用余弦定理

总共有三种情况

• 完全相离,面积为 0
• 中心重合,面积就是大圆减小圆
• 其他情况,需要4部分相加减计算得出

代码

/*
By:OhYee
Github:OhYee
Blog:http://www.oyohyee.com/
Email:oyohyee@oyohyee.com

かしこいかわいい？
エリーチカ！
要写出来Хорошо的代码哦~
*/
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <string>
#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <functional>
#include <bitset>
using namespace std;

const int maxn = 45;
const int maxm = 1000005;
const double pi = 3.141592653589;
int a[maxn];
int dp[maxn][maxm];

struct O {
    double x;
    double y;
    double r;
    O(double x,double y,double r) {
        this->x = x;
        this->y = y;
        this->r = r;
    }
};
inline double Ha(double a,double b,double c) {
    double p = (a + b + c) / 2;
    double ans = sqrt(p*(p - a)*(p - b)*(p - c));
    return ans;
}
inline double distance(double x1,double y1,double x2,double y2) {
    double ans = sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2));
    return ans;
}
inline double Sshanxing(double r,double h) {
    double th = asin(h / r);
    return th  * r *r / 2;
}
inline double Ssanjiao(double h,double r) {
    return sqrt(r*r - h*h)*h / 2;
}
inline double Syuan(double r) {
    return pi*r*r;
}


inline double S(O o1,O o2) {
    double dis = distance(o1.x,o1.y,o2.x,o2.y);
    if(dis + 1e-8 > o2.r + o1.r)
        return 0;
    if(dis < fabs(o2.r - o1.r) + 1e-8) {
        double r = min(o1.r,o2.r);
        return pi * r * r;
    }


    double costh1 = (o1.r*o1.r + dis*dis - o2.r*o2.r) / (2 * o1.r*dis);
    double costh2 = (o2.r*o2.r + dis*dis - o1.r*o1.r) / (2 * o2.r*dis);
    double th1 = acos(costh1);
    double th2 = acos(costh2);
    return th1*o1.r*o1.r + th2*o2.r*o2.r - o1.r*dis*sin(th1);

    /*double h = Ha(o1.r,o2.r,dis) / dis * 2;
    double S1 = Sshanxing(o1.r,h) - Ssanjiao(h,o1.r);
    double S2 = Sshanxing(o2.r,h) - Ssanjiao(h,o2.r);
    double s = (S1 + S2) * 2;
    return s;*/
}

void Do() {
    double r,R;
    double x1,x2,y1,y2;
    scanf("%lf%lf",&r,&R);
    scanf("%lf%lf",&x1,&y1);
    scanf("%lf%lf",&x2,&y2);

    O o1x(x1,y1,r);
    O o1d(x1,y1,R);
    O o2x(x2,y2,r);
    O o2d(x2,y2,R);

    double ans = S(o1d,o2d) - S(o1x,o2d) - S(o1d,o2x) + S(o1x,o2x);

    printf("%.6f\n",ans);
}

int main() {
    int T;
    scanf("%d",&T);
    for(int i = 1;i <= T;i++) {
        printf("Case #%d: ",i);
        Do();
    }
    return 0;
}