题目

Description

After the king's speech , everyone is encouraged. But the war is not over. The king needs to give orders from time to time. But sometimes he can not speak things well. So in his order there are some ones like this: "Let the group-p-p three come to me". As you can see letter 'p' repeats for 3 times. > > Poor king!

Now , it is war time , because of the spies from enemies , sometimes it is pretty hard for the general to tell which orders come from the king. But fortunately the general know how the king speaks: the king never repeats a letter for more than 3 times continually .And only this kind of order is > > legal. For example , the order: "Let the group-p-p-p three come to me" can never come from the king. While the order:" Let the group-p three come to me" is a legal statement.

The general wants to know how many legal orders that has the length of n

To make it simple , only lower case English Letters can appear in king's order , and please output the answer modulo 10000000071000000007

We regard two strings are the same if and only if each charactor is the same place of these two strings are the same.

Input

The first line contains a number T(T≤10)T(T≤10)――The number of the testcases.

For each testcase, the first line and the only line contains a positive number n(n≤2000)n(n≤2000).

Output

For each testcase, print a single number as the answer.

Sample Input

2
2
4

Sample Output

676
456950

hint:

All the order that has length 2 are legal. So the answer is 26*26. For the order that has length 4. The illegal order are : "aaaa" , "bbbb"…….."zzzz" 26 orders in total. So the answer for n == 4 is 26^4-26 = 456950

题解

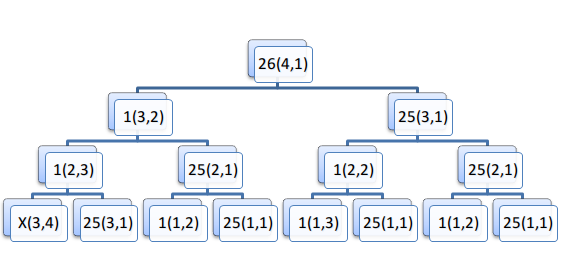
排列问题，计算26个字母，最多有3个连续的情况个数

将字符所在的层数(其后还有多少个字符)和字符已经连续了多少次，看作状态条件

可以发现每种状态存在关联，而且不相互影响

将每条分支乘上去，加起来即是所求的答案

可以发现其中有重读的计算(如(2,1))

因此，可以采用动态规划的记忆化搜索

n为层数 m为连续数目
dp[n][m]=dp[n-1][m+1]+dp[n-1][m]*25

dp[n-1][m+1]代表选择和上一位一样的

dp[n-1][m]代表选择和上一位不一样的

其边界条件就是n=0和m=4

由于达到边界时，应该返回1，因此应该让dp[0][m!=1]来返回1，dp[0][1]返回0(会乘上25)

如果m=4时，要返回0，说明不能再往下走

由于数据较大，因此需要mod 1000000007

而且在10层左右时，就需要开始取余数，而我们可能要算到2000层
因此，每一次更新值都需要进行取余操作

(a+b) mod c = ((a mod c) + (b mod c)) mod c
(a*b) mod c = ((a mod c) * (b mod c)) mod c

根据该定理，可以将更新操作写成

(dp[n][m] = (DP(n - 1, m + 1) % mod) + ((25 * (DP(n - 1, 1) % mod)) % mod)) % mod;

最后在输入n后，26*dp[n][1]就是我们需要的答案

代码

/*
By:OhYee
Github:OhYee
Email:oyohyee@oyohyee.com
Blog:http://www.cnblogs.com/ohyee/

かしこいかわいい？
エリーチカ！
要写出来Хорошо的代码哦~
*/
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <string>
#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <stack>
using namespace std;

//DEBUG MODE
#define debug 0

//循环
#define REP(n) for(int o=0;o<n;o++)

const int mod = 1000000007;
const int maxn = 2005;
typedef unsigned long long LL;
LL dp[maxn][5];

//n层数 m连续数目
LL DP(int n, int m) {
    if (n == 0) {
        if (m == 1)
            return 0;
        else
            return 1;
    }

    if (m == 4)
        return 0;

    if (dp[n][m] == 0) {
        //(a+b) mod c = ((a mod c) + (b mod c)) mod c
        //(a*b) mod c = ((a mod c) * (b mod c)) mod c
        return (dp[n][m] = (DP(n - 1, m + 1) % mod) + ((25 * (DP(n - 1, 1) % mod)) % mod)) % mod;
    }
    else {
        return dp[n][m];
    }

}

void Do() {
    int n;
    scanf("%d", &n);
    LL ans = (DP(n, 1) % mod) * 26;
    printf("%llu\n", ans % mod);
    return;
}


int main() {
    memset(dp, 0, sizeof(dp));
    int T;
    scanf("%d", &T);
    while (T--) {
        Do();
    }
    return 0;
}