吐槽一句，这个东西好难拼

迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。——百度百科

Dijkstra算法就是用来算在一个有向带权图中，一个点到其他各点的最短距离

其思路是：

1. 给起始点权值标成0，其他点标成无限大。从出发点开始
2. 向该点向能通向的点走，算出到各点的总距离，并标记在相应点上。
3. 给该点标记上访问标志，以后不再访问该点，然后从所有点中选出权值最小的点，重复步骤2
4. 当所有点均被标记后，各点权值即为到该点最短距离

代码
我觉得我写的好冗杂，不过注释应该能看懂的，理会意思即可

#include <iostream>
#include <set>
#include <vector>
#include <queue>
using namespace std;


class Dijkstra{
    private:
        const int INF=100000;
        struct Edge{//边
            int to,weight;
        };
        struct Weight{//用于优先队列的比较
            int weight,n;
            bool operator < (const Weight& rhs)const{
                return weight>rhs.weight;//权值越大，优先度越小
            }
        };

        struct Tree{//树
            vector<vector<Edge> > node;
            vector<int> d;//到各个节点的最小值
            int N;//节点数目

            void init(int NodeNumber){//初始化
                node.resize(NodeNumber);
                d.resize(NodeNumber);
                N=NodeNumber;
            }

            void Add(int from,int to,int weight){//添加边
                node[from].push_back((Edge){to,weight});
            }
        };
        Tree T;

    public:
        void Add(int from,int to,int weight){
            T.Add(from,to,weight);
        }
        void init(int NodeNumber){
            T.init(NodeNumber);
        }
        void dijkstra(int v){//Dijkstra主算法
            vector<int>done;//访问标记
            done.resize(T.N);
            for(int i=0;i<T.d.size();i++){
                T.d[i]=INF;
                done[i]=0;
            }
            priority_queue <Weight> Q;//优先队列
            Q.push((Weight){0,v});//从第一个点开始
            T.d[v]=0;

            //BFS
            while(!Q.empty()){//只要队列不空就走下去
                int u=Q.top().n;//获得优先度最高的节点
                Q.pop();
                if(done[u])continue;//如果已经访问过就跳过
                done[u]=1;//访问标记
                for(int i=0;i<T.node[u].size();i++){//该节点可以访问的节点
                    Edge& next=T.node[u][i];
                    if(T.d[u]+next.weight<T.d[next.to]){//如果距离更短，则更新
                        T.d[next.to]=T.d[u]+next.weight;
                        Q.push((Weight){next.weight,next.to});
                        //可以在这里加上一个vector，用来记录路径
                    }
                }
            }
        }
        int get(int n){//返回到达指定节点的最短距离
            return T.d[n];
        }
};

int main(){
   Dijkstra D;
   D.init(6);
   D.Add(0,1,7);
   D.Add(0,2,9);
   D.Add(0,5,14);
   D.Add(1,0,7);
   D.Add(1,2,10);
   D.Add(1,3,15);
   D.Add(2,0,9);
   D.Add(2,1,10);
   D.Add(2,3,11);
   D.Add(2,5,2);
   D.Add(3,1,15);
   D.Add(3,2,11);
   D.Add(3,4,6);
   D.Add(4,3,6);
   D.Add(4,5,9);
   D.Add(5,0,14);
   D.Add(5,0,14);
   D.Add(5,4,9);
   D.dijkstra(0);

   for(int i=0;i<6;i++){
        cout<<D.get(i)<<endl;
   }

}

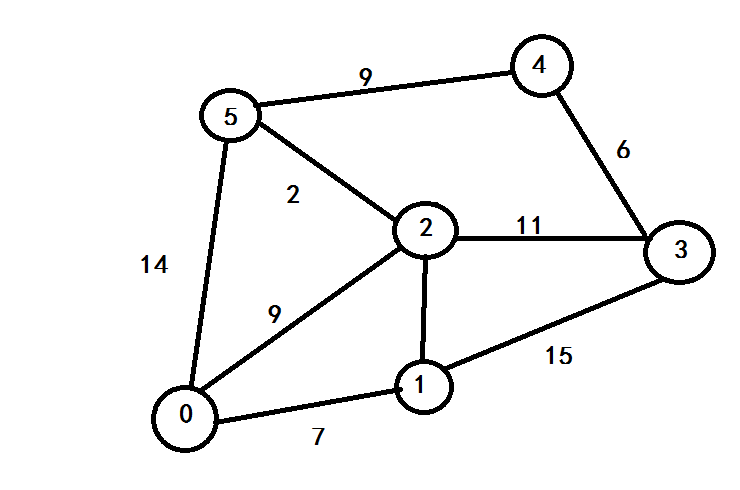
这个程序实现了如图所示图的最短距离的求得